智能卡加密算法的微分能量分析方法研究

文章出處：http://www.nyfzw.net 作者：胡勇, 沈庭芝, 郭濤, 李守鵬   人氣： 發表時間：2011年09月30日

    1 引言

    智能卡作為一種安全可靠的高技術產品, 在我國正逐步取代磁卡而廣泛應用于金融行業以及其他相關產業。但部分用戶在對智能卡產品的認識上存在著一些誤區, 片面地認為所有擁有微處理器的智能卡都具有高安全性和高可靠性, 從而忽略了這方面的要求。事實上針對智能卡的攻擊方法伴隨著智能卡的發展而發展, 一直威脅著智能卡的安全。

    目前比較流行的是稱作能量分析的攻擊方法, 它分為兩類: 簡單能量分析( SPA)和微分能量分析( DPA)。SPA是一種直接解釋能量消耗測定值的技術。系統消耗能量的大小隨微處理器執行的指令不同而不同, 當微處理器在對加密算法的不同部分執行運算時, 能量消耗變化有的會很明顯。借助這種特征, 攻擊者能區分出單條指令, 達到破解算法的目的。DPA 的攻擊力比SPA 強得多, 而且更加難以防范, 它不像SPA從系統的能量消耗直觀地作出判斷, 而是借助統計方法來提取與密鑰有關的信息。盡管實現的過程更加復雜, 但降低了對攻擊者的智能卡專業技術水平的要求。

    2 微分能量分析

    在密碼的運算過程中, 智能卡執行一條指令所消耗的能量與指令的操作數相關。如果用PI 表示指令I 執行過程中平均消耗的能量, op₁ , op₂ , ..., op_n 表示I 的操作數, 當op₁ 取不同值時, 有 

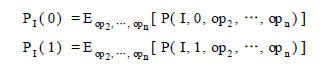
    稱P_I 與op₁ 相關, 即P_I ( 0) ≠ P_I ( 1) 。微分能量分析正是從這種相關性著手, 最終實現對加密密鑰的破解。設P_I ( 0 ) , P_I ( 1)的差值為D_I , D_I 越大, 對作DPA 分析越有利。一階微分能量分析往往采用以下步驟:

    ( 1) 確立類似于op₁ 的操作數或中間變量, 取值為α。要求根據已知智能卡信息( 明文、密文) D 和未知的密鑰信息能夠推導出它的值, 即α= f( K, D) 。

    ( 2) 對多組不同明文分別進行加密, 對相應的能量信號進行采樣并記錄波形。

    ( 3) 對K 的值進行猜測, 計算出相應的α, 將( 2) 中的采樣結果按照α= 0 和α= 1 分成兩組, 求兩組的均值差( 即構建統計函數) 。α時刻均值差最大時, K猜測正確。從以上步驟我們可以看出, 攻擊者要發動DPA 攻擊, 需要具備以下條件: 熟悉智能卡中采用的加密算法原理結構; 知道智能卡處理的明文或者是處理后的密文; 有相應的硬件條件,用于測量能量消耗軌跡。圖1 就是實施DPA 攻擊的基本電路。 

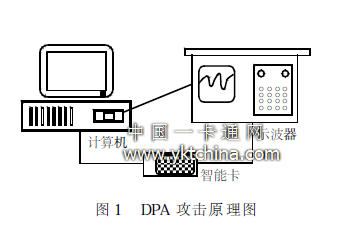
    3 智能卡常用加密算法的DPA 攻擊

    根據加密機制的不同, 加密算法可以分為兩類: 對稱加密算法和非對稱加密算法。智能卡中常用的加密算法, 如DES,3DES, RSA 和ECC 等都可以歸結到這兩類算法中。DPA 最先是在針對智能卡的對稱加密算法的破解方法研究中發現的, 但隨后就發現它對破解非對稱加密算法同樣有效。下面我們分別就這兩類算法中最具代表性的算法: DES 和ECC 來對DPA攻擊進行分析。

    3. 1 DES 的DPA 攻擊

    DES 是對稱密碼體制中最典型的一個例子, 它是由IBM 公司公布的一種加密算法, 1977 年被美國國家標準局確立為 聯邦數據加密標準后完全公開, 是世界上技術最成熟的加密算 法。DES 在加密時, 將明文分成長度為64 位的由0、1 組成的 串, 使用的密鑰長度為64 位。DES 采用了Feistel 網絡結構, 有 16 個迭代周期, 每個周期按照公式( 1) 迭代: 

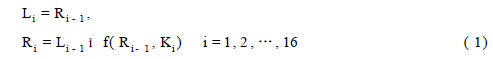
    其中, f( R _{i - 1} , K _i ) = P( S( E( R _{i - 1} ) ī K _I ) ) , K _i 表示第i 個迭代周期的密鑰。迭代過程如圖2 所示。 

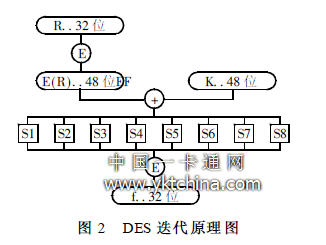
     在對DES 進行DPA 分析時, 我們選定的中間操作數是第16 輪迭代過程輸入L15 值中的一位, 設為d。d 與已知信息、待求密鑰之間的關系如下式所示: 

    其中, b 為R ₁₆ 中由d 經過加密得到的二進制位。C* 為R15 中輸入S* 的比特位。在每個迭代過程中, 密鑰被分成了八個二進制密鑰塊, 分別對應一個S 盒, S* 是d 對應的S 盒。K*₁₆ 是輸入S* 的六位二進制密鑰塊, K ₁₆ 中的一部分。K^*₁₆ 是破解的對象, 作為六位的二進制密鑰塊, 它的取值無非有64 種, 這其中當然包括正確的密鑰。下面的工作就是要結合實際觀測找出該密鑰。

    假設DES 算法加密不同的明文時觀測到的能量信號為Sij( i 表示明文編號, j 表示時間) 。明文數量為N 時, 針對K*16 的每一種猜測就會有N 個觀測結果, 由式( 2) 計算出d 值, 根據d值對觀測結果分類, 如下所示: 

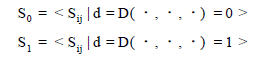
    假定S₀ 和S₁ 的均值差為T[ j] , 考慮到S₀ 和S₁ 是隨機能量信號集合分出的兩個子集, 唯一的區別是加密進行到d 時d的取值不同, 因而S₀ 和S₁ 的均值是有差異的。對于T[ j] , 如果猜測密鑰正確, 則在d 處理時刻T[ j] 會出現一個峰值, 與d無關的時刻, T[ j] 趨于零; 如果密鑰錯誤, 由函數D 得出的d值可能與真值不符, 導致部分Sij 不能正確歸入S₀ 和S₁ , 削弱了d 時刻應有的能量差異性, T[ j] 在這個時刻即使有峰值, 也無法與密鑰正確時相比。不過相同的是在d 以外的點, T[ j] 仍然趨于零。因此, 找出64 個當中含有最大峰值的T[ j] 軌跡,其對應的密鑰塊即為K*₁₆ 。重復上述過程對其余七個S 盒進行分析, 就可以得出第16 輪使用的48 位密鑰。要破解整個DES 密鑰, 只需對前面各輪進行同樣分析即可。

    3. 2 ECC 的DPA 攻擊

   公開密鑰算法通常基于一個數學上的難題, 橢圓曲線加密算法也不例外。考慮等式K = kG( K, G 是橢圓曲線上的點, k為小于G 的階的整數) , 不難發現, 給定k 和G, 根據橢圓曲線加法法則, 計算K 很容易; 但給定K 和G, 求k 就相對困難了。

    我們把點G 稱為基點, k 稱為私有密鑰, K 稱為公開密鑰。ECC 主要涉及的是類似kG 的點乘運算, 該運算在智能卡芯片中用指令實現時, k 往往寫成二進制擴展形式, 即k = k _{n - 1} k _{n - 2}...k₀ , 而kG 則用連加的形式代替, 如下列代碼所示: 

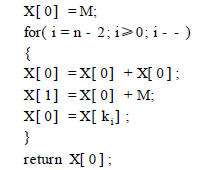
    其中, “+ ”是橢圓曲線上的加法, 運算法則與普通加法不同。從代碼可以看出當循環運算進行到i 時, X[ 0] 的值僅與k的二進制擴展表示中的( k _{n - 1} , ..., k _i ) 有關。如果X[ 0] 的中間結果用pM表示( p 是整型系數, 隨For 循環遞增, 可能的取值取決于k _i ) , 那么運算過程中的能量消耗將與pM 二進制表示中的位相關。例如, 為了獲取k 的二進制位k _{n - 2} , 我們可以考查4M中的位與能量信號的相關性。對N 個不同的M分別執行上述指令操作, 觀測它們的能量信號軌跡, 記作S _i。選定4M二進制表示中的一個比特位( 如第二位b₂ ) 作為對S _i 進行分組的依據:

    S₀ = < S_i | b₂ = 0 >

    S₁ = < S_i |b₂ = 1 >

    設S₀ 和S₁ 的均值差為C( t) , 從它的軌跡就可以判斷出k _{n - 2}的值。原因在于: d _{n- 2} = 0 時, 4M是中間結果, S_i 與b₂ 相關, 在b₂ 對應時刻C( t) 出現峰值; d _{n - 2} = 1 時, 4M不是中間結果, S₀ 和S₁ 的均值不再有明顯差異, C( t) 不會出現峰值。依此類推, 我們可以獲取k 二進制表示中剩余各位的值。

    4  AES 候選算法與DPA 攻擊

    DES 使用的密鑰因為太短, 無法滿足安全要求, 正逐步走向末路。AES是美國國家標準技術研究所( NIST) 發起征集的旨在取代DES 的高級數據加密標準。它的基本要求是: 必須是私鑰分組加密算法, 密鑰長度至少為128 位。本文提到的AES 候選算法特指入圍第二輪評選的五種算法( Twofish  ,Rijndael , Serpent , MARS, RC6 ) , 它們都有自己獨特的設計思路和風格, 對許多目前流行的攻擊方法有相當的抵抗能力, 但這并不包括DPA 攻擊。

    ( 1) Twofish 加密算法使用16 輪的Feistel 網絡結構, 在網絡的輸入和輸出運用了白化處理技術。這種技術原理比較簡單, 就是將待隱藏數據和特定密鑰進行“加”或“異或”運算, 但產生的加密效果很強, 攻擊者因此而得不到核心部分的輸入輸出。在利用DPA 對Twofish 進行分析時, 關鍵在于獲取白化過程中采用的密鑰。統計分析建立在如下基礎上: 當白化密鑰位是0 時, 對應輸入的明文二進制位保持不變; 當白化密鑰位是1 時, 對應輸入的明文二進制位取反。我們可以對多組明文進行加密, 采集能量信號, 求出128 位白化密鑰對應的明文二進制位與能量信號的協方差函數, 由于兩者主要是在異或前讀取數據, 異或和異或后寫入結果時刻相關, 故協方差函數波形中有不多的幾個峰值。主要觀察的是異或前讀取數據和異或后寫入結果時刻對應的峰值, 兩個峰值方向相同表示密鑰是0,反之則表示密鑰是1。在獲取白化過程使用的密鑰后, 接下來是希望通過Twofish 密鑰生成算法推導出核心過程密鑰, 但這無法直接實現, 只能是結合密鑰生成算法和白化過程密鑰將核心過程密鑰取值范圍縮小后逐一驗證。

    ( 2) Rijndael 采用的是代替/ 置換網絡, 當加密分組和密鑰長度都為128 位時, 加密輪數是10。加密開始時, 輸入分組的各字節按特定的方式裝入一個矩陣State 中, 接下來是一個與密鑰的異或操作, 不僅僅是在輪加密開始之前, 在每輪加密之中和輪加密之后都有類似的操作, 只是采用的密鑰不同, 但它們都是由Rijndael 密鑰生成算法統一生成。第一次的異或操作密鑰完全可以通過DPA 攻擊獲取, 然后根據Rijndael 密鑰生成算法直接推出其余各輪的密鑰, 這與Twofish 相比要簡單得多。

    ( 3) Serpent 是一個在初始置換和末尾置換之間安排有32輪加密操作的算法, 沒有采用白化技術, 每一輪包含密鑰混合運算、S- 盒及線性變換。針對Serpent 完全可以采用前面介紹的針對DES 類似的DPA 分析。考慮到利用Serpent 的密鑰生成算法推出其余各輪密鑰, 必須預知兩輪以上的子密鑰, 這就意味著攻擊者至少要破解32 輪中前面至少兩輪以上的加密過程。

    由此可見, Twofish, Rijndael, Serpent 只要利用簡單的幾輪DPA 分析得來的子密鑰, 結合統一的相對獨立的密鑰生成算法, 就可以用來破解主密鑰和其他的子密鑰。但同樣的方法對MARS 和RC6 并不適用, 這主要在于它們的密鑰生成算法設計獨特, 使得密鑰間的遞推難以實現, 這就迫使攻擊者必須對這兩種算法的核心加密過程展開分析。加密算法總是由基本操作組成的, 這些操作抵御能量攻擊的能力差異較大, 與Twofish, Rijndael, Serpent 相比, MARS 和RC6 包含了較多比較脆弱的操作, 如異或、查表、輪移、算術運算( 加、減、乘) 等, 有些更適合用SPA 進行分析。MARS 和RC6 算法設計者采用白化技術的初衷就是為了增強對核心過程的保護。攻擊者一旦采用DPA 技術解除了這種保護功能, 便能結合SPA, DPA 直接對核心部分展開分析, 破解其中的密鑰。 

    (文/1. 北京理工大學電子工程系, 北京100081; 2. 華中科技大學計算機科學系, 湖北武漢430074; 3. 中國信息安全測評認證中心, 胡勇1 , 沈庭芝1 , 郭濤2 , 李守鵬3)